Note
The following implementation and documentation is based on the work of F. Musciotto, L. Marotta, S. Miccichè, and R. N. Mantegna Bootstrap validation of links of a minimum spanning tree.
Bootstrapping¶
Bootstrapping is a statistical method used to resample a dataset with replacement to estimate its population statistics (such as mean, median, standard deviation, etc.) In machine learning applications, bootstrap sampling usually leads to less overfitting and improvement of the stability of our models. Bootstrap methods draw small samples (with replacement) from a large dataset one at a time, and organizing them to construct a new dataset. Here we examine three bootstrap methods. Row, Pair, and Block Bootstrap.
Note
Underlying Literature
The following sources elaborate extensively on the topic:
Bootstrap validation of links of a minimum spanning tree by Musciotto, F., Marotta, L., Miccichè, S. and Mantegna, R.N.
Row Bootstrap¶
The Row Bootstrap method samples rows with replacement from a dataset to generate a new dataset. For example, for a dataset of size \(T \times n\) which symbolizes \(T\) rows (timesteps) and \(n\) columns (assets), if we use the row bootstrap method to generate a new matrix of the same size, we sample with replacement \(T\) rows to form the new dataset. This implies that the new dataset can contain repeated data from the original dataset.
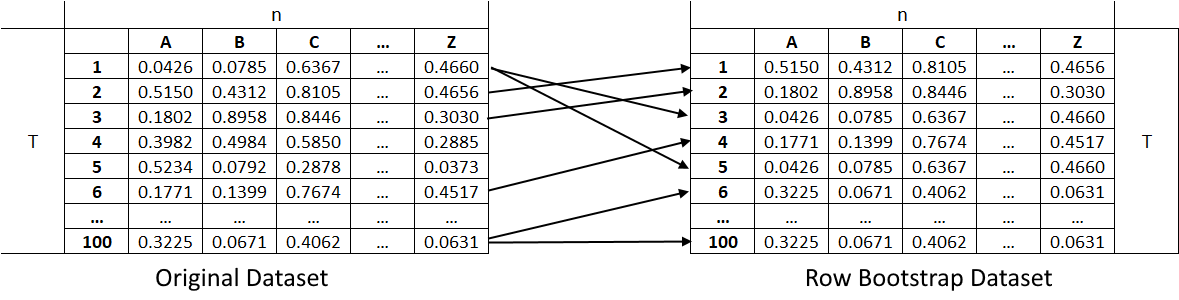
(Left) Original dataset of size \(T \times n\). (Right) Row bootstrap dataset of size \(T \times n\).¶
Implementation¶
Example¶
Pair Bootstrap¶
The Pair Bootstrap method samples pairs of columns with replacement from a dataset to generate a new dataset. This new dataset can be used to generate a dependence matrix, as is a correlation matrix. For example, for a dataset of size \(T \times n\) which symbolizes \(T\) rows (timesteps) and \(n\) columns (assets), if we use the pair bootstrap method to generate a correlation matrix of size \(n \times n\), we iterate over the upper triangular indices of the correlation matrix. For each index, we sample with replacement 2 columns and all their rows. We calculate the correlation measure of this pair and use it to fill the given index of the correlation matrix. We repeat this process until we fill the correlation matrix.

(Left) Original dataset of size \(T \times n\). (Right) Row bootstrap dataset, each of size \(T \times 2\). Each pair dataset can be used to generate a dependence matrix (e.g. correlation matrix).¶
Implementation¶
Example¶
Block Bootstrap¶
The Block Bootstrap method samples blocks of data with replacement from a dataset to generate a new dataset. The block size can be of a size equal to or less than the original dataset. The blocks in this module are non-overlapping (except on the edges of the dataset if the blocks cannot perfectly split the data). Their ideal size depends on the data and its application. For example, for a dataset of size \(T \times n\) which symbolizes \(T\) rows (timesteps) and \(n\) columns (assets), if we use the Block Bootstrap method to split the data set into blocks of \(2 \times 2\), then we sample as many blocks as needed to fill the bootstrapped matrix.
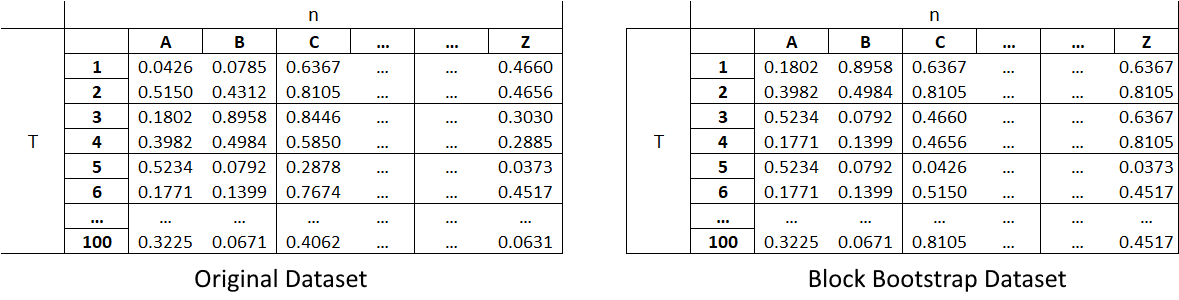
(Left) Original dataset of size \(T \times n\). (Right) Block bootstrap dataset of size \(T \times n\) created with blocks of size \(2 \times 2\).¶
Implementation¶
Example¶
Research Notebook¶
The following research notebook can be used to better understand the bootstrap methods.


