Sequential Bootstrapping¶
The key power of ensemble learning techniques is bagging (which is bootstrapping with replacement). The key idea behind bagging is to randomly choose samples for each decision tree. In this case, trees become diverse and by averaging predictions of diverse trees built on randomly selected samples and random subset of features data scientists make the algorithm much less prone to overfit.
However, in our case, we would not only like to randomly choose samples but also choose samples which are unique and non-concurrent. But how can we solve this problem? Here comes the Sequential Bootstrapping algorithm.
The key idea behind Sequential Bootstrapping is to select samples in such a way that on each iteration, we maximize the average uniqueness of selected subsamples.
Implementation¶
The core functions behind Sequential Bootstrapping are implemented in MlFinLab and can be seen below:
Example¶
An example of Sequential Bootstrap using a toy example from the book can be seen below.
Consider a set of labels \(\left\{y_i\right\}_{i=0,1,2}\) where:
label \(y_0\) is a function of return \(r_{0,2}\)
label \(y_1\) is a function of return \(r_{2,3}\)
label \(y_2\) is a function of return \(r_{4,5}\)
The first thing we need to do is to build an indicator matrix. Columns of this matrix correspond to samples, and rows correspond to price returns timestamps which were used during samples labelling. In our case indicator matrix is:
One can use get_ind_matrix method from the MlFinLab package to build an indicator matrix from triple-barrier events.
We can get average label uniqueness on indicator matrix using get_ind_mat_average_uniqueness function from MlFinLab.
Let’s get the first sample average uniqueness (we need to filter out zeros to get unbiased results).
As you can see, it is quite close to values generated by get_av_uniqueness_from_triple_barrier function call.
Let’s move back to our example. In the Sequential Bootstrapping algorithm, we start with an empty array of samples (\(\phi\)) and loop through all samples to get the probability of choosing the sample based on the average uniqueness of the reduced indicator matrix constructed from [previously chosen columns] + sample.
For performance increase, we optimized and parallelized for-loop using numba, which corresponds to bootstrap_loop_run function.
Now let’s finish the example:
To be as close to the MlFinLab implementation, let’s convert ind_mat to numpy matrix.
1st Iteration:
In the first step, all labels will have equal probabilities as the average uniqueness of the matrix with 1 column is 1. Say we have chosen 1 on the first step.
2nd Iteration
Probably the second chosen feature will be 2 (prob_array[2] = 0.43478, which is the largest probability). As you can see, up till now, the algorithm has chosen two the least concurrent labels (1 and 2).
3rd Iteration
Sequential Bootstrapping tries to minimise the probability of repeated samples so, as you can see, the most probable sample would be 0 with 1 and 2 already selected.
4th Iteration
The most probable sample would be either 1 or 2 in this case.
After 4 steps of sequential bootstrapping, our drawn samples are [1, 2, 0, 2].
Let’s see how this example is solved by the MlFinLab implementation. To reproduce that:
we need to set warmup to [1], which corresponds to phi = [1] on the first step
verbose = True to print updated probabilities
As you can see, the first 2 iterations of the algorithm yield the same probabilities, however sometimes the algorithm randomly chooses not the 2 sample on 2nd iteration that is why further probabilities are different from the example above. However, if you repeat the process several times, you’ll see that on average drawn sample equal to the one from the example.
Sparse Indicator Matrix and Bootstrapping¶
Warning
The sequential bootstrap model from the MlFinlab package before version 1.4.0 was already orders of magnitude faster than the original, described in Advances in Financial Machine Learning.
We’ve further improved the model, starting from MlFinLab version 1.5.0 the execution is up to 3000 times quicker compared to the models from version 1.4.0 and earlier. (The speed improvement depends on the size of the input dataset)
By using the sparse, transposed indicator matrix, it’s possible to achieve a significant increase in performance over the standard method, that uses the indicator matrix construction from the Advances in Financial Machine Learning book.
The below code piece shows how to use the sparse indicator matrix for bootstrapping.
Monte-Carlo Experiment¶
Let’s see how sequential bootstrapping increases average label uniqueness on this example by generating 3 samples using sequential bootstrapping and 3 samples using standard random choice, repeat the experiment 10000 times and record corresponding label uniqueness in each experiment.
KDE plots of label uniqueness support the fact that sequential bootstrapping gives higher average label uniqueness.
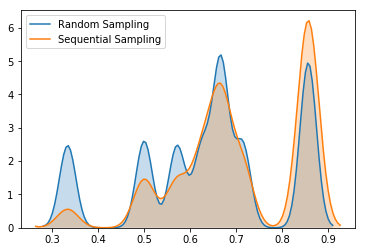
We can compare average label uniqueness using sequential bootstrap vs label uniqueness using standard random sampling by setting compare parameter to True. We have massively increased the performance of Sequential Bootstrapping, which was described in the book. For comparison generating 50 samples from 8000 barrier-events would take 3 days, we have reduced time to 10-12 seconds which decreases by increasing number of CPUs.
Let’s apply sequential bootstrapping to our full data set and draw 50 samples:
Sometimes you would see that standard bootstrapping gives higher uniqueness, however as it was shown in Monte-Carlo example, on average Sequential Bootstrapping algorithm has higher average uniqueness.
Research Notebook¶
The following research notebooks can be used to better understand the previously discussed sampling methods




